Multi-Level Deep Q-Networks: Taking Reinforcement Learning Forward
The field of reinforcement learning (RL) has significantly transformed machine learning by allowing agents to acquire optimal behaviors via their interactions with the environment. Deep Q-Networks (DQNs) have advanced RL by integrating deep neural networks for the purpose of approximating Q-values, which fundamentally serve to forecast the long-term value associated with executing a particular action in a specified state. This blog article discusses the groundbreaking concept of Multi-Level Deep Q-Networks, a complex technique that builds on the capabilities of standard DQNs, especially challenging problems.
Deep Q-Networks
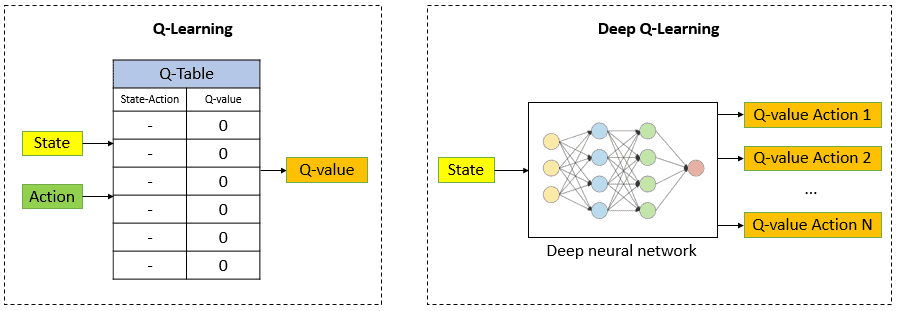
First, one needs to have a good grasp of the underlying principles that govern them: Deep Q-Networks. DQNs approximate the Q-function by using a neural network; it’s the mathematical expression of states as it correlates to the expected cumulative rewards of any possible action that might be performed. In simple terms, it predicts the long-term value of various actions within a particular situation.
It acquires knowledge through the reduction of the gap between the Q-values that it predicts and the rewards it gets from the environment. Learning in this context is essentially an adjustment of the weights of the network based on experience, leading to progressive improvement in the accuracy of the Q-value estimates. There is the concept of “dual actions.” The dual action at any time takes into consideration the current action along with its Q-value and a target action along with its target Q-value. An important constituent of the update logic of the network is formed by the dual action approach, which allows it to learn and enhance its Q-value estimations over time.
Multi-Level DQNs
Although DQNs have been very successful in many applications, they can face challenges in complex environments, especially those with delayed rewards or hierarchical structures. In such scenarios, traditional DQNs may fail to learn effectively because it is hard to propagate rewards over extended time horizons or across different levels of abstraction.
A major challenge of DQNs when deployed in complex settings is that they become unstable due to the use of function approximation.
In a high-dimensional space where there exist too many states, it is impractical to hold Q-values for all state-action pairs. It is in such a space that function approximations, specifically neural networks in this case, come into use to approximate the Q-values within DQNs. But such can lead to instability in learning especially with the use of off-policy TD learning algorithms like Q-learning. There has been some innovation in designing M-DQNs that attempt to overcome some of these problems. One major innovation in M-DQNs is its hierarchical structure in which a number of DQNs operate at various levels of abstraction.
This multi-level approach enables an agent to break up complex tasks into smaller, more manageable sub-tasks, thereby achieving more efficient learning and performance. The hierarchical organization does not only enhance the efficiency of learning but also mitigates some problems that arise due to the instability of traditional DQNs in approximating functions. Through distributing the learning process across many levels, M-DQNs will be more equipped to handle complexities from high-dimensional environments and may overcome the problem of instability related to function approximation.
How Multi-Level DQNs Work
Typically, M-DQNs make use of a hierarchical structure which consists of a top-level DQN and one or more sub-level DQNs. The top-level DQN controls high-level decisions by providing a global view of the whole task, whereas the sub-level DQNs control particular sub-tasks or components of the environment. The sub-level DQNs learn to accomplish intermediate goals; their outputs are fed into the top-level DQN, which then determines the final action to be taken.
There are many important benefits of the hierarchical framework:
- Better Learning Efficiency: M-DQNs break up complex tasks into smaller sub-tasks, which makes them have a higher learning efficiency especially in environments where rewards are deferred. This subdivision allows the agent to focus on learning specific aspects of the task, leading to faster convergence and a significant increase in overall performance.
- Generalization: Was improved as the hierarchical framework would allow policies learned to be generally applicable in other scenarios. This is due to the fact that the sub-tasks can learn independently and use their acquired knowledge in varying contexts, not bound by changes to the superordinate task or environment.
- Better Management of Complex Environments: M-DQNs outperform in managing complex environments with hierarchical structures or multiple sub-tasks. The multi-layered approach enables the agent to explore and learn in these complex environments, breaking down the complexity into more manageable pieces.
In addition, M-DQNs apply the principle of “multiple Q functions” to enhance the stability of the learning procedure. The use of multiple Q functions enables the network to better stabilize the target value that is utilized in the updating of Q-value estimations. This approach assists in minimizing the impact of significant changes in one Q function on the other functions, thus resulting in a more robust and reliable learning process.
Another way it extends the ability to learn more effectively is through experience sharing among agents in a multi-agent DQN. For example, the “N-DQN Experience Sharing” algorithm is one such example of how a collection of agents might share their experiences, learn from others and in turn become better than themselves. Such acceleration on part of the agents leads to greater overall performance.
Use Cases of Multi-Level DQNs
M-DQNs have been quite effective in various applications across multiple domains:
- Robotics:
M-DQNs can be applied in the field of robotics to control robotic systems in complex environments and enable them to perform various tasks such as navigation, object manipulation, and human-robot interaction. The hierarchical structure allows the robot to break down complex actions into a series of simpler sub-tasks, thus improving its ability to learn and adapt to new situations. - Game Playing:
M-DQNs have been very successful in hierarchical structured games like strategy games and role-playing games. In such games, the agent has to take decisions at several levels of abstraction, ranging from the individual action of units up to overall strategic planning. The M-DQNs can be applied effectively to this type of hierarchical decision-making process. - Finance:
M-DQNs can be applied in algorithmic trading where they learn to make the best investment decision based on market data and sentiment analysis. For example, a multi-level DQN can be used for historical Bitcoin price data and Twitter sentiment analysis to predict future price movements and make proper trading decisions. - Healthcare:
There are applications in healthcare for reinforcement learning models, and possibly the M-DQNs. The models can be tested based on some metrics like F-measure (F), G-mean (G), Area Under the Receiver Operating Characteristic curve (AUROC), Sensitivity, and Specificity. These can be used in evaluating the models’ performance for tasks such as disease prediction and optimization of the treatment.
Note that the architecture of an M-DQN depends on the application. A common structure is a top-level DQN and one or more lower-level DQNs, but the number of levels and how they interact can be adapted to suit the specific needs of the task.
One way to better illustrate the concept of M-DQNs is through the following analogy: Imagine learning how to cook a complicated recipe. Instead of trying to learn the whole recipe at once, one might break it up into smaller sub-tasks, such as chopping vegetables, preparing the sauce, and preparing the main ingredients. Each of these sub-tasks can be learned separately, and then combined together to form the final dish.
This is very similar to how M-DQNs work, because each level of the network focuses on a different aspect of the overall task.
Research Papers on Multi-Level DQNs
Given the increased interest in M-DQNs, there are several research papers discussing their potential and applications. A few of them include:
- Multi-Agent Deep Q Network to Enhance the Reinforcement Learning for Delayed Reward System:
This study presents a multi-agent Deep Q Network (N-DQN) framework designed to enhance the efficacy of reinforcement learning in contexts characterized by delayed rewards. The authors illustrate the success of their methodology through experiments conducted in a maze navigation task and a ping-pong game, both scenarios incorporating delayed reward mechanisms. - Bitcoin Trading Strategy Using Multi-Level Deep Q-Networks:
This paper introduces an M-DQN method for Bitcoin trading based on the history of prices and analysis of the sentiments on Twitter. The authors show that their model of M-DQN can achieve higher profits with risks reduced significantly as compared to standard trading strategies. - Advancing Algorithmic Trading: A Multi-Technique Enhancement of Deep Q-Network Models:
This paper improves a DQN trading model by incorporating the most advanced methodologies, including Prioritized Experience Replay, Regularized Q-Learning, Noisy Networks, Dueling, and Double DQN. The authors show superior performance of their enhanced model over several assets, including BTC/USD and AAPL.
The studies above have contributed key ideas toward the theoretical foundations and pragmatic instantiations of M-DQNs that will pave the way for future developments in this space.
Comparison to Other DQN Variants
M-DQNs differ from a backdrop of other DQNs due to its unique hierarchical nature of structure and approach in solving complex tasks. Among the other DQNs for comparison are the following:
- Feature
- M-DQN
- Hierarchical DQN (HDQN)
- Double DQN
| Structure | Multiple DQNs in a hierarchical fashion | Single DQN with hierarchical action selection | Two DQNs for action selection and evaluation |
|---|---|---|---|
| Focus | Decomposition of complex tasks | Learning hierarchical policies | Reduction of overestimation of Q-values |
| Applications | Complex environments with delayed rewards, hierarchical structures | Tasks with hierarchical structure, long-term planning | General reinforcement learning tasks |
Conclusion
Multi-level Deep Q-Networks are significant developments in reinforcement learning, giving a very viable method to handle complex tasks and heterogeneous environments. The hierarchical framework, splitting up the complexity of the problems into more solvable sub-tasks, further exhibits M-DQNs’ ability to be very efficient learners and superior in generalization capabilities as well. Furthermore, it increases the stability and efficiency of learning with experience sharing and use of multiple Q functions.
M-DQNs have shown very promising results in many domains, including robotics, game playing, finance, and healthcare. As research in this area continues, we can expect even more innovative applications of M-DQNs in the future that will push the boundaries of what’s possible with reinforcement learning.
For a broader perspective and additional insights into the world of reinforcement learning, you can also read Reinforcement Learning: A Full Overview. Discover how these groundbreaking innovations, including Multi-Level Deep Q-Networks, are shaping the future of AI!





